1.1 Q-4
Question Statement
Find the domain and the range of the following functions and sketch their graphs:
i.
ii.
iii.
iv.
v.
vi.
vii.
viii.
Background and Explanation
To solve these types of questions, you need to understand the concepts of domain and range:
- Domain: The set of all possible input values (x-values) for which the function is defined.
- Range: The set of all possible output values (y-values) the function can take based on its domain.
Additionally, sketching the graph of a function helps visualize its behavior, providing insights into how the function changes across its domain.
Solution
i.
- Domain: The function is a linear function, so it is defined for all real values of .
- Domain:
- Range: A linear function produces all real values for , so the range is also all real numbers.
- Range:
Graph:
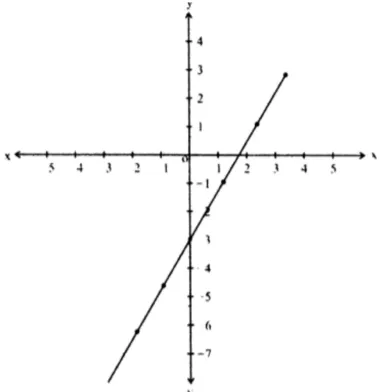
- Range:
Graph:
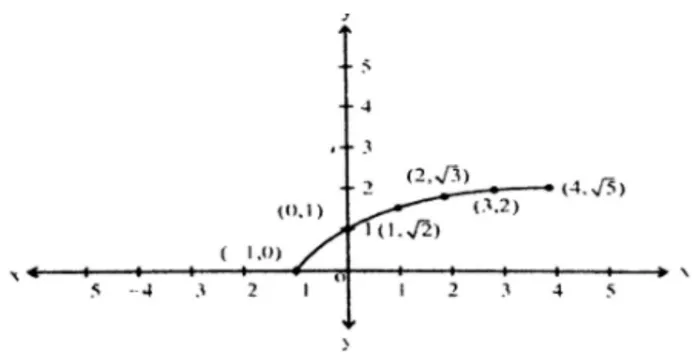
ii.
- Domain: The expression inside the square root must be non-negative, i.e., .
Solving this gives or .- Domain:
- Range: Since the square root produces non-negative values, the range is all non-negative real numbers.
- Range:
Graph:
- Range:
Graph:
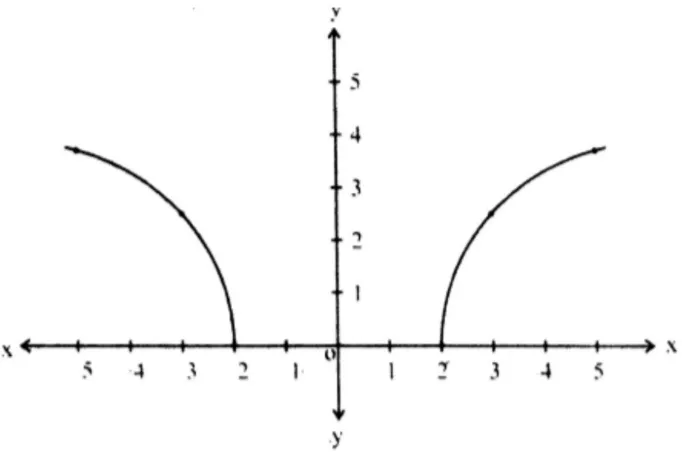
iii.
- Domain: The expression inside the square root must be non-negative, i.e., .
Solving this gives .- Domain:
- Range: Since the square root produces non-negative values, the range is all non-negative real numbers.
- Range:
Graph:
- Range:
Graph:
iv.
- Domain: Absolute value functions are defined for all real values.
- Domain:
- Range: Since the absolute value is always non-negative, the range is all non-negative real numbers.
- Range:
Graph:
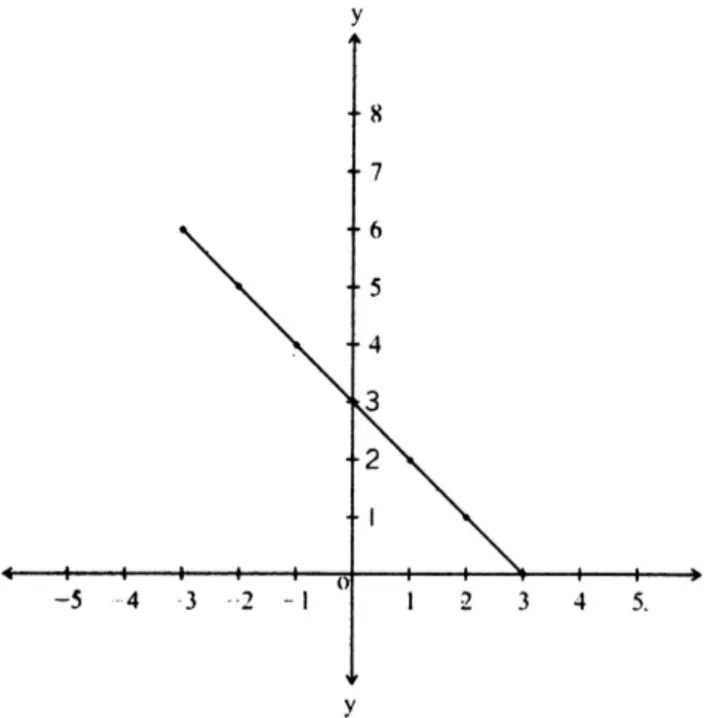
- Range:
Graph:
v.
- Domain: The piecewise function is defined for all real numbers, excluding any gaps.
- Domain:
- Range: Since both parts of the function can take all real values, the range is all real numbers.
- Range:
Graph:
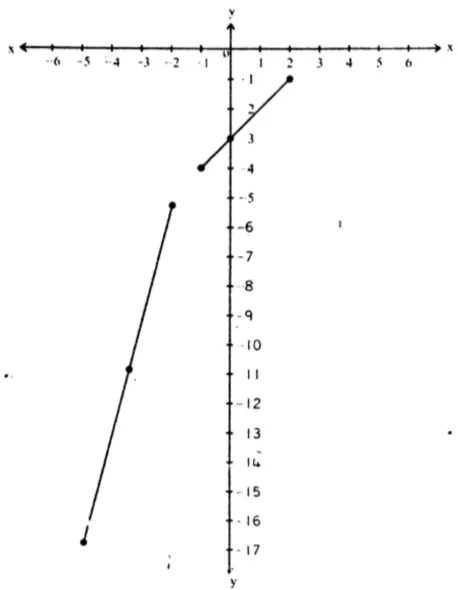
- Range:
Graph:
vi.
- Domain: The piecewise function is defined for all real values of .
- Domain:
- Range: Since both parts of the function can take all real values, the range is all real numbers.
- Range:
Graph:
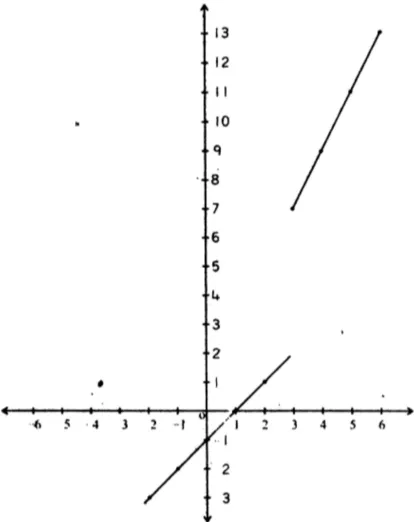
- Range:
Graph:
vii.
-
Domain: The denominator cannot be zero, so .
- Domain:
-
Range: Since the simplified form of the function is , the range is all real values except .
- Range:
Graph:
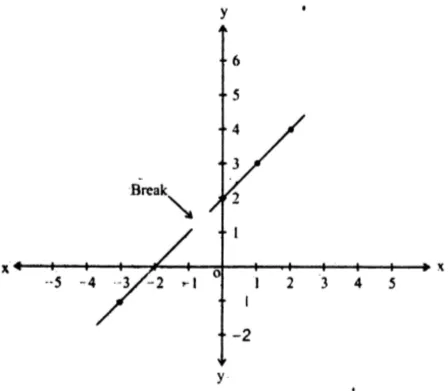
viii.
- Domain: The denominator cannot be zero, so .
- Domain:
- Range: Since the function can take all real values except at , the range is all real numbers except .
- Range:
Graph:
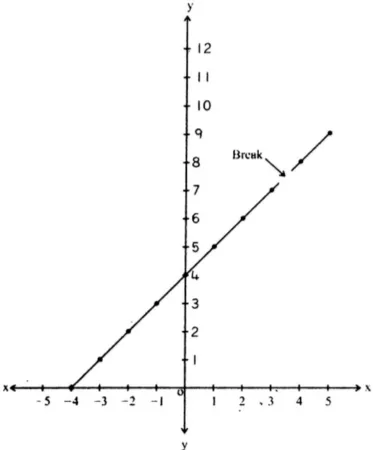
- Range:
Graph:

