04_Ex 6.4

Exercise Questions

Questions	Links
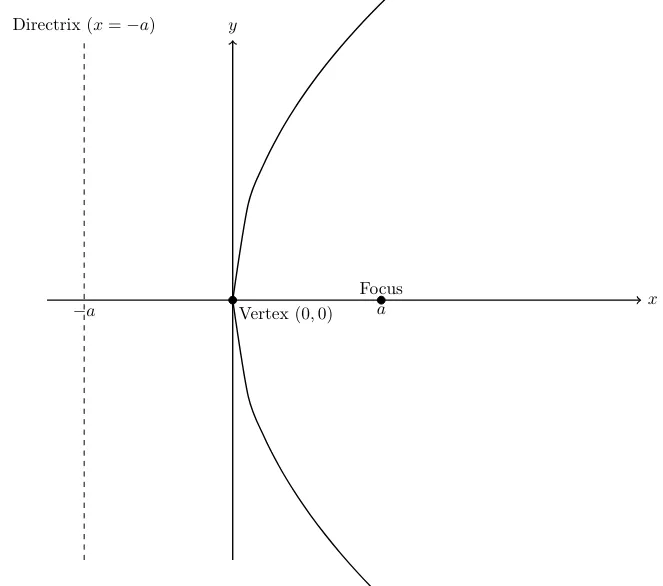
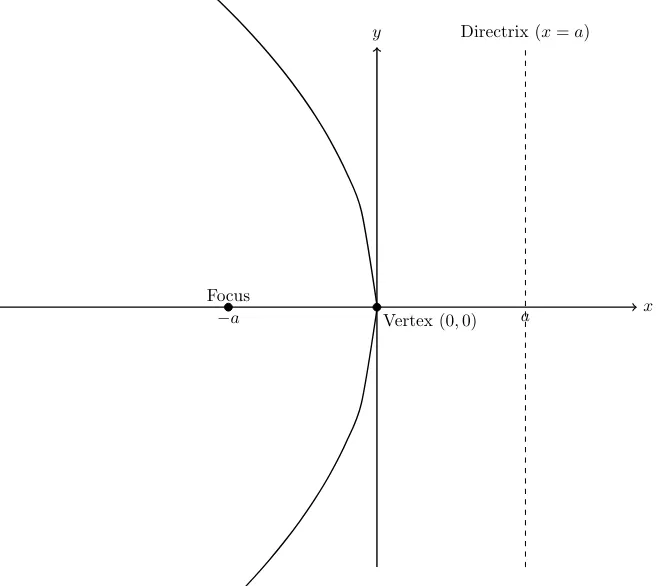
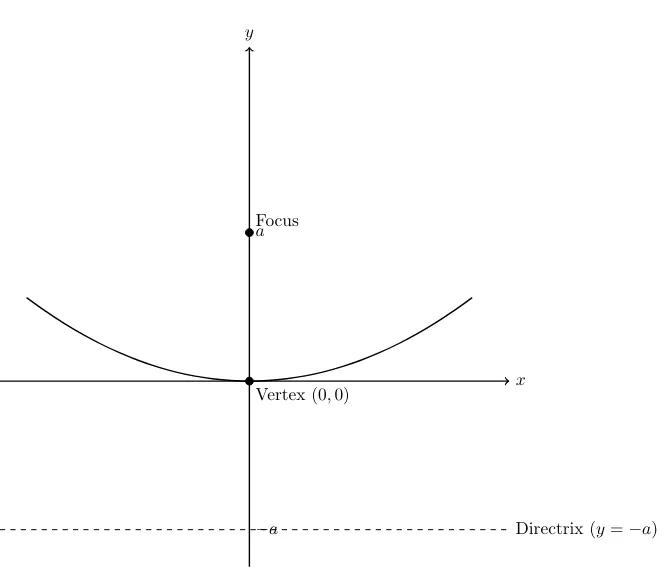
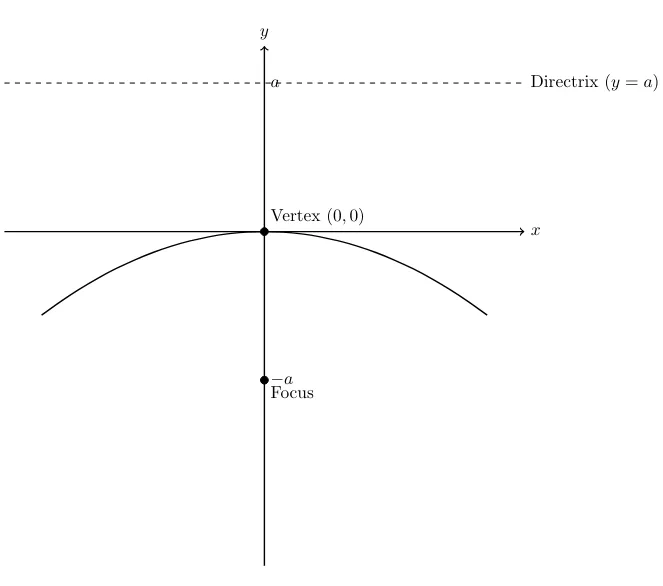
Q1. Find the focus, vertex and direction…	6.4 Q-1
Q2. Write an equation for the parabola with given…	6.4 Q-2
Q3. Find the equation of parabola having its focus…	6.4 Q-3
Q4. Show that the parabola having…	6.4 Q-4
Q5. Show that the ordinate at any point $P$…	6.4 Q-5
Q6. A comet has a parabolic orbit with the earth…	6.4 Q-6
Q7. Find an equation of the parabola formed by…	6.4 Q-7
Q8. A parabola arch has 100 m base and height 25 m…	6.4 Q-8
Q9. Show that tangent at any point $P$ of…	6.4 Q-9

---

Overview

This exercise focuses on understanding and applying the key concepts of linear and quadratic functions, including their graphing techniques and properties. Linear functions result in straight-line graphs, while quadratic functions form parabolas. The exercise emphasizes identifying critical features such as slopes, intercepts, and vertices, which are foundational in graphing and solving these functions. These concepts have broad applications in algebra, geometry, and real-world modeling scenarios.

---

Key Concepts

1. Linear Functions

• Definition: A linear function is of the form $f(x) = mx + c$, where $m$ is the slope and $c$ is the y-intercept.
• Graph: A straight line with a constant slope.
• Slope: The rate of change of $y$ with respect to $x$, calculated as:

$$m = \frac{y_2 - y_1}{x_2 - x_1}$$

• Intercepts:
  • X-intercept: Point where the line crosses the x-axis ($y = 0$).
  • Y-intercept: Point where the line crosses the y-axis ($x = 0$).

2. Quadratic Functions

• Definition: A quadratic function is of the form $f(x) = ax^2 + bx + c$, where $a \neq 0$.
• Graph: A parabola that opens upward if $a > 0$ and downward if $a < 0$.
• Vertex: The point where the parabola changes direction, given by:

$$x = -\frac{b}{2a}$$

• Intercepts:
  • X-intercepts: Roots of the equation $f(x) = 0$, calculated using the quadratic formula:

$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$

 - **Y-intercept**: Value of $f(0) = c$.

---

Important Formulas

1. Linear Functions:
   • Slope formula:

$$m = \frac{y_2 - y_1}{x_2 - x_1}$$

• Equation of a line (point-slope form):

$$y - y_1 = m(x - x_1)$$

2. Quadratic Functions:
   • Standard form:

$$f(x) = ax^2 + bx + c$$

• Vertex form:

$$f(x) = a(x - h)^2 + k$$

 where $(h, k)$ is the vertex.

• Quadratic formula:

$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$

---

Tips and Tricks

• Intercept Method: Use intercepts to quickly sketch the graph of a function.
• Vertex Form for Quadratics: Rewrite the quadratic equation in vertex form to easily identify the vertex and the direction of the parabola.
• Slope Interpretation: For linear functions, interpret the slope as the steepness of the line and its direction.
• Quadratic Direction: Analyze the coefficient $a$ to determine whether the parabola opens upwards ($a > 0$) or downwards ($a < 0$).

---

Summary

This exercise emphasizes mastering the foundational concepts of linear and quadratic functions, including their graphing and properties. Understanding slopes, intercepts, and vertices is essential for solving equations and modeling real-world problems. By practicing these techniques, students will build a solid understanding of these critical algebraic tools.

---

Reference

By Sir Shahzad Sair:

---

Graphs

==$y^2=4ax$==

---

$y^2=-4ax$

---

$x^2=4ay$

---

$x^2=-4ay$

---