05_Ex 6.5

Exercise Questions

Questions	Links
Q1. Find an equation for the ellipse with given…	6.5 Q-1
Q2. Find the centre, foci, eccentricity, vertices, directrices…	6.5 Q-2
Q3. Let '$a$' be a positive number and $\mathbf{0}<\mathbf{c}<$ a…	6.5 Q-3
Q4. Use Question 3 to find equation of the ellipse…	6.5 Q-4
Q5. Define the latus rectum of an ellipse…	6.5 Q-5
Q6. The major axis of an ellipse is standard form…	6.5 Q-6
Q7. An asteroid has elliptic orbit with the sun…	6.5 Q-7
Q8. An arc in the shape of a semi ellipse in 90 m…	6.5 Q-8
Q9. The moon orbits the earth in an elliptic path…	6.5 Q-9

---

Overview

This exercise delves into the properties and equations of ellipses, focusing on their standard forms, geometric definitions, and key applications. Ellipses are critical in various fields such as astronomy, physics, and engineering due to their unique reflective and geometric properties. This exercise emphasizes understanding how to derive equations of ellipses based on given parameters, compute their elements, and analyze their geometric behavior.

---

Key Concepts

Diagram

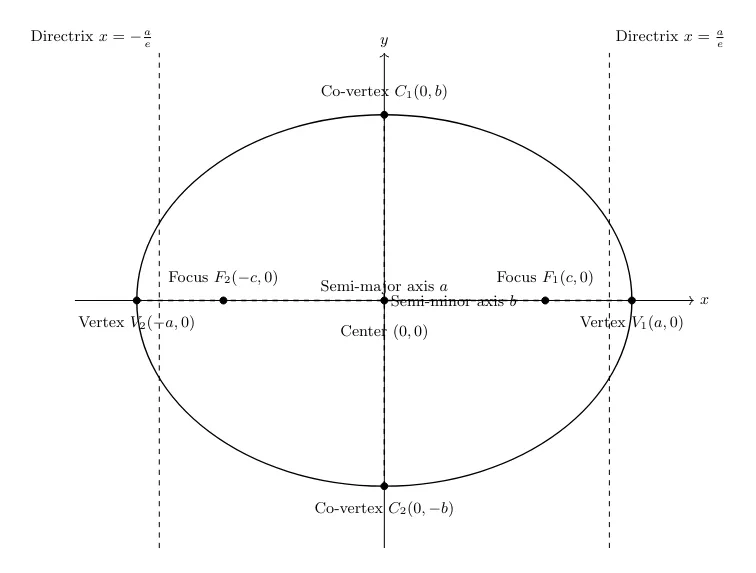
Ellipse Definition

• Ellipse: The locus of points where the sum of the distances from two fixed points (foci) is constant.
• Center: Located at the midpoint of the line joining the foci, often at the origin $(0, 0)$.
• Vertices: Points where the ellipse intersects the major axis.
• Co-Vertices: Points where the ellipse intersects the minor axis.

Geometric Elements

• Major Axis: The longest diameter of the ellipse.
• Minor Axis: The shortest diameter of the ellipse.
• Foci: Points located along the major axis at a distance $c$ from the center, where $c^2 = a^2 - b^2$.
• Eccentricity ($e$): A measure of the ellipse’s “ovalness,” calculated as $e = \frac{c}{a}$, with $0 < e < 1$.

Standard Equation

The standard equation of an ellipse is:

$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$

• For a horizontal ellipse, $a > b$, and the major axis is along the x-axis.
• For a vertical ellipse, $b > a$, and the major axis is along the y-axis.

---

Important Formulas

Topic	Formula
Major Axis Length	$2a$
Minor Axis Length	$2b$
Eccentricity	$e = \frac{c}{a}$
Relationship Between Axes	$c^2 = a^2 - b^2$

---

Tips and Tricks

1. Identify Orientation: Use the coefficients of the ellipse equation to determine whether it is horizontal or vertical.
2. Graphing Accuracy: Accurately locate the foci, vertices, and co-vertices to graph the ellipse.
3. Symmetry: Leverage the symmetry of the ellipse about its axes for quick calculations and graphing.
4. Parameter Relationships: Understand how $a$, $b$, and $c$ relate to simplify computations.

---

Summary

Understanding ellipses involves mastering their geometric definitions, deriving their equations, and analyzing their properties. These concepts form the foundation for tackling real-world problems involving ellipses, from orbital mechanics to structural design.

---

Reference

By Sir Shahzad Sair:

---