1.5 Q-3
Question Statement
Draw the graph of the functions defined below and find whether they are continuous.
i.
Background and Explanation
This problem involves piecewise functions where the rule for changes depending on the value of . To determine continuity, we need to check whether there are any discontinuities at the boundary where the function switches from one rule to the other.
Solution
For the first part of the problem, let’s first compute the values for when using .
| -1 | 0 | 1 | 2 | |
|---|---|---|---|---|
| -2 | -1 | 0 | 1 |
Points:
For , the function follows .
| 3 | 4 | 5 | 6 | |
|---|---|---|---|---|
| 7 | 9 | 11 | 13 |
Points:
The graph shows two different lines representing the function. Hence, the function is discontinuous at .
Graph:
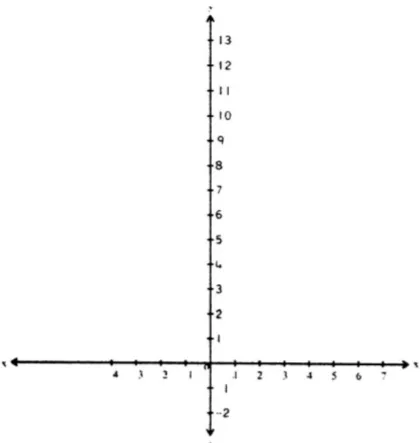
ii.
Solution
Simplifying the given equation:
Factoring gives us:
Domain: The function is undefined at , so we exclude it from the domain. Let’s prepare the table for some values of in the domain:
| -4 | -3 | -2 | -1 | 0 | 1 | 1.5 | 2 | 2.5 | 3 | 4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| -2 | -1 | 0 | 1 | 2 | 3 | 3.5 | — | 4.5 | 5 | 6 |
Graph:
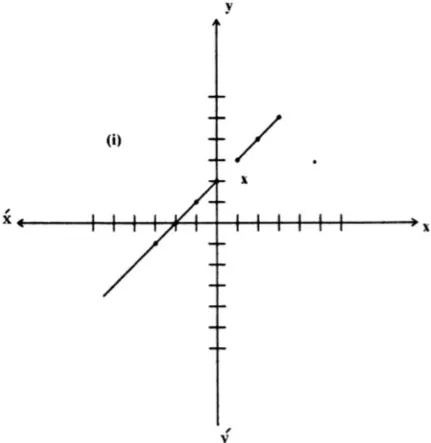
The graph is a straight line with a hole at the point , as the function is undefined at . The graph shows a discontinuity at .
iii.
Solution
Here, the function follows two different rules. For , the function is . For , the function is .
We now prepare the table for values of in the domain:
| -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 2 | 7 | 8 |
Graph:
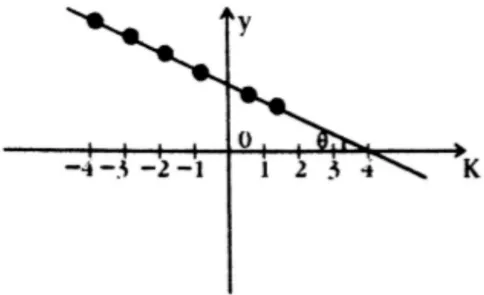
The graph is a straight line with a break at , where the function jumps from to . This shows a discontinuity at .
iv.
Solution
Simplifying the equation:
Factoring gives:
Domain: The function is undefined at . Let’s prepare the table for some values of in the domain:
| -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3.5 | 4 | 4.5 | 5 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7.5 | — | 8.5 | 9 |
Graph:
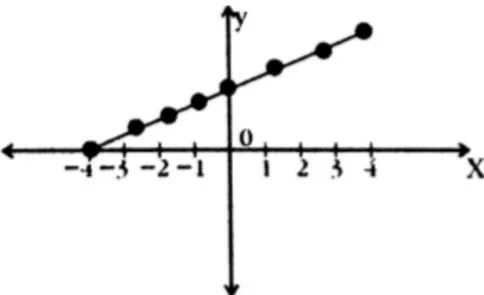
The graph is a straight line with a hole at the point , showing a discontinuity at .
Key Formulas or Methods Used
- Piecewise functions: Where different rules are applied to different intervals.
- Simplification of rational expressions to find the continuous form of the function.
- Checking continuity by inspecting the graph for breaks or holes at specific points.
Summary of Steps
- For each function, express the given function in simplified form if possible.
- Prepare a table with values of and for the domain.
- Plot the points and analyze whether the function has any discontinuities.
- Verify the graph and determine whether the function is continuous or discontinuous at specific points.

