1.5 Q-4

Question Statement

Find the graphical solutions of the following equations:

1. $x = \sin(2x)$
2. $\frac{x}{2} = \cos(x)$
3. $2x = \tan(x)$

---

Background and Explanation

To solve these types of problems graphically, we typically plot both sides of the equation and identify the points where the two curves intersect. The x-values of the intersection points represent the solutions to the equation. We are working with three different trigonometric equations here, each with a different type of curve. For each equation, we break the interval into smaller subintervals and calculate the corresponding values of both sides, followed by plotting and finding the intersection points.

---

Solution

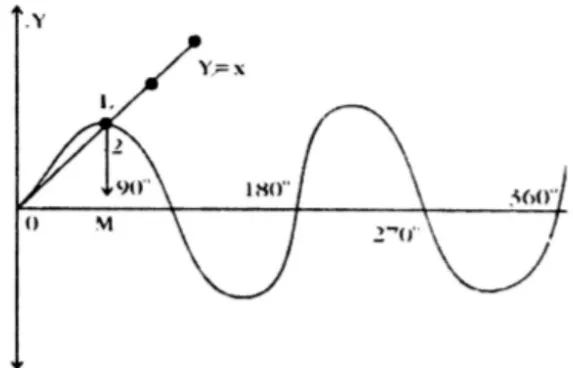
i. $x = \sin(2x)$

We are solving for the interval $[0, 2\pi]$. Consider subintervals of length $\frac{\pi}{6}$. The table below shows the values for $x$ and $\sin(2x)$:

$x$	$0^\circ$	$30^\circ$	$60^\circ$	$90^\circ$	$120^\circ$	$150^\circ$	$180^\circ$
$\sin(2x)$	0	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{3}}{2}$	0	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{3}}{2}$	0

$x$	$210^\circ$	$240^\circ$	$270^\circ$	$300^\circ$	$330^\circ$	$360^\circ$
$\sin(2x)$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{3}}{2}$	0	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{3}}{2}$	0

By drawing perpendiculars from the points on the x-axis where the curves intersect, we can read the angles at $10^\circ$ and $55^\circ$, which are the solutions.

Graphical Intersection: The common solutions are $x = 10^\circ$ and $x = 55^\circ$.

---

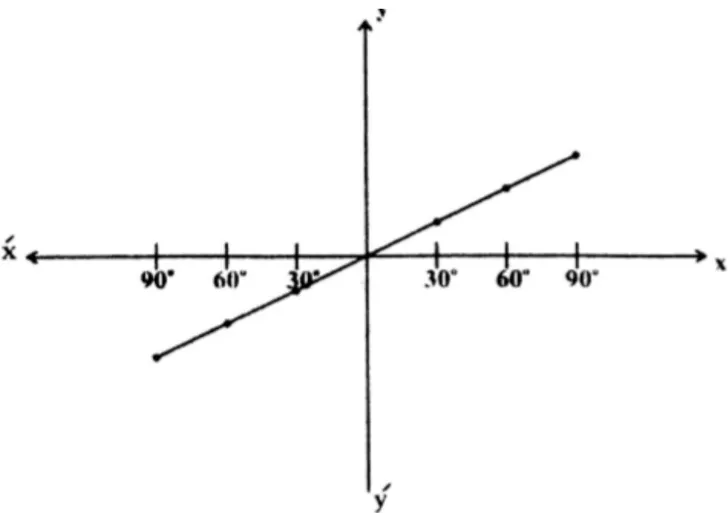
ii. $\frac{x}{2} = \cos(x)$

We are solving for the interval $(0, \pi)$. Again, consider subintervals of length $\frac{\pi}{6}$. The table below shows the values for $\frac{x}{2}$ and $\cos(x)$:

$x$	$0^\circ$	$30^\circ$	$60^\circ$	$90^\circ$	$120^\circ$	$150^\circ$	$180^\circ$
$\frac{x}{2}$	0	$\frac{\pi}{12}$	$\frac{\pi}{6}$	$\frac{\pi}{4}$	$\frac{\pi}{3}$	$\frac{5\pi}{12}$	$\frac{\pi}{2}$
$\cos(x)$	1	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	0	$-\frac{1}{2}$	$-\frac{\sqrt{3}}{2}$	-1

By drawing perpendiculars from the points on the x-axis where the curves intersect, we can read the angle at $67^\circ$, which is the solution.

Graphical Intersection: The common solution is $x = 67^\circ$.

---

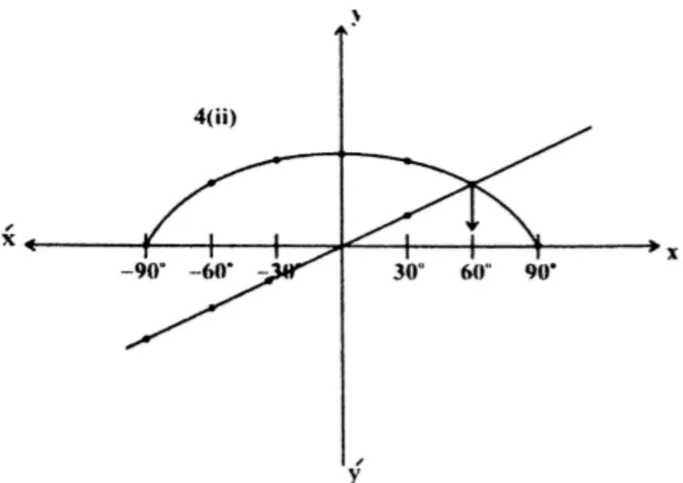
iii. $2x = \tan(x)$

We are solving for the interval $[0, \pi]$. Again, consider subintervals of length $\frac{\pi}{6}$. The table below shows the values for $2x$ and $\tan(x)$:

$x$	$0^\circ$	$30^\circ$	$60^\circ$	$90^\circ$	$120^\circ$	$150^\circ$	$180^\circ$
$2x$	0	$\frac{\pi}{3}$	$\frac{2\pi}{3}$	$\pi$	$\frac{4\pi}{3}$	$\frac{5\pi}{3}$	$2\pi$
$\tan(x)$	0	$\frac{1}{\sqrt{3}}$	$\sqrt{3}$	$\infty$	$-\sqrt{3}$	$-\frac{1}{\sqrt{3}}$	0

By drawing perpendiculars from the points on the x-axis where the curves intersect, we can observe that the solutions are near the values $0^\circ$ and $60^\circ$.

Graphical Intersection: The common solutions are $x = 0^\circ$ and $x = 60^\circ$.

---

Key Formulas or Methods Used

• Trigonometric identities: For the equations $\sin(2x)$, $\cos(x)$, and $\tan(x)$, their respective graphing methods are used.
• Graphical method: Plotting the functions and finding their points of intersection visually.
• Perpendicular dropping: Using perpendiculars from the intersection points on the x-axis to read the angles.

---

Summary of Steps

1. For $x = \sin(2x)$:

   • Use subintervals of $\frac{\pi}{6}$.
   • Create the table for $x$ and $\sin(2x)$.
   • Identify intersection points at $10^\circ$ and $55^\circ$.

2. For $\frac{x}{2} = \cos(x)$:

   • Use subintervals of $\frac{\pi}{6}$.
   • Create the table for $\frac{x}{2}$ and $\cos(x)$.
   • Identify intersection point at $67^\circ$.

3. For $2x = \tan(x)$:

   • Use subintervals of $\frac{\pi}{6}$.
   • Create the table for $2x$ and $\tan(x)$.
   • Identify intersection points at $0^\circ$ and $60^\circ$.

---

Reference