5.3 Q-2

Question Statement

Maximize the function $f(x, y) = x + y$ subject to the constraints:

$$2y + 5x \leq 30$$ $$5x + 4y \leq 20$$ $$x \geq 0, \quad y \geq 0$$

---

Background and Explanation

To solve this problem, we are dealing with a linear programming optimization problem. The objective is to maximize the function $f(x, y) = x + y$ under the given constraints. The constraints define a feasible region, and we will use graphical methods to determine the maximum value of the objective function within this region.

---

Solution

Step 1: Convert constraints into equations

We first work with the two inequalities by converting them into equalities to identify boundary lines.
For the first inequality, $2y + 5x \leq 30$:

$$2x - 5y = 30$$

For the second inequality, $5x + 4y \leq 20$:

$$5x - 4y = 20$$

Step 2: Find the intersection points for each equation

We substitute $x = 0$ and $y = 0$ into the equations to find points of intersection:

For the first equation $2x - 5y = 30$:

• When $x = 0$, $5y = 30 \Rightarrow y = 6$. Hence, the point is $(0, 6)$.
• When $y = 0$, $2x = 30 \Rightarrow x = 15$. Hence, the point is $(15, 0)$.

For the second equation $5x - 4y = 20$:

• When $x = 0$, $-4y = 20 \Rightarrow y = 5$. Hence, the point is $(0, 5)$.
• When $y = 0$, $5x = 20 \Rightarrow x = 4$. Hence, the point is $(4, 0)$.

Step 3: Determine feasibility of the region

We check if the points $(0,0)$, $(4,0)$, and $(0,5)$ satisfy the original constraints.

• Substituting $(0,0)$ into both equations shows that the inequalities hold true.
• Substituting $(4,0)$ into both equations also satisfies the inequalities.
• Substituting $(0,5)$ shows that the inequalities are true as well.

Thus, these points are valid and form the feasible region. The graph below shows the shaded region where these points lie.

---

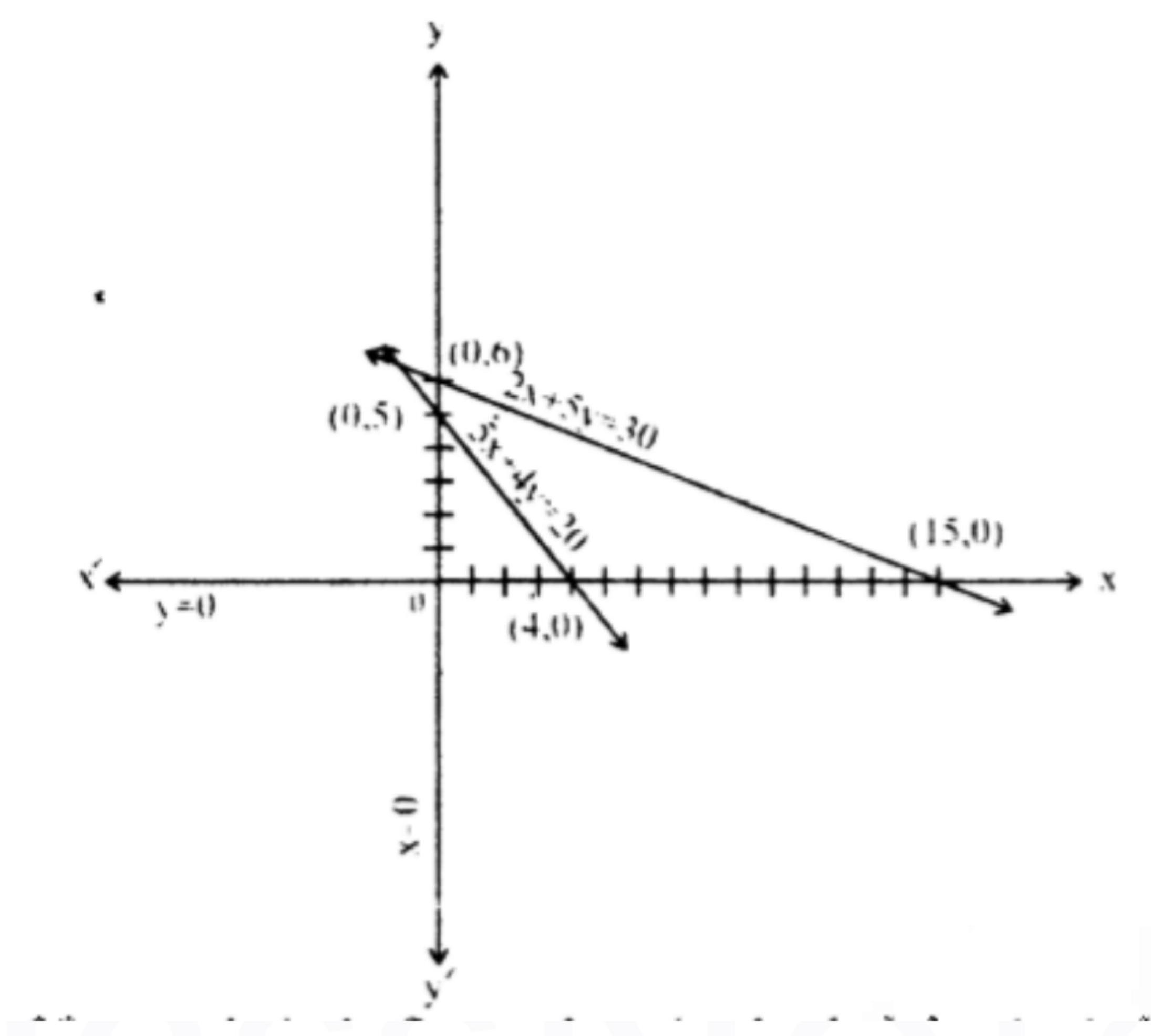
Key Formulas or Methods Used

• Constraints conversion into equalities to find boundary lines.
• Substitution method to find intersection points of the constraints.
• Feasibility check to ensure that the intersection points satisfy all constraints.

---

Summary of Steps

1. Convert the inequalities into equations:
   $2x - 5y = 30 \quad \text{and} \quad 5x - 4y = 20$

2. Find the intersection points for each equation by substituting $x = 0$ and $y = 0$:

   • For $2x - 5y = 30$: $(0,6)$ and $(15,0)$.
   • For $5x - 4y = 20$: $(0,5)$ and $(4,0)$.

3. Check the feasibility of the region formed by the points $(0,0)$, $(4,0)$, and $(0,5)$.

4. Evaluate the objective function $f(x, y) = x + y$ at the corner points:

   • At $(4,0)$, $f(4,0) = 4$.
   • At $(0,5)$, $f(0,5) = 15$.
   • At $(0,0)$, $f(0,0) = 0$.

5. The maximum value of the function is 15, occurring at the point $(0,5)$.

---