5.3 Q-4

Question Statement

Maximize the objective function: $z = 2x + y$

Subject to the following constraints:

$$x + y \leq 3$$ $$7x + 5y \leq 35$$ $$x \geq 0$$ $$y \geq 0$$

---

Background and Explanation

This problem involves linear programming, where we aim to maximize a given objective function subject to several linear constraints. The steps typically involve:

1. Graphing the inequalities to find the feasible region.
2. Identifying the corner points (vertices of the feasible region).
3. Evaluating the objective function at these points to determine the maximum or minimum value.

---

Solution

1. Graph the constraints:

   • Constraint 1: $x + y \leq 3$
     Rewrite as $x + y = 3$.

     • Set $x = 0$: $y = 3$. Point: $(0, 3)$.
     • Set $y = 0$: $x = 3$. Point: $(3, 0)$.

   • Constraint 2: $7x + 5y \leq 35$
     Rewrite as $7x + 5y = 35$.

     • Set $x = 0$: $5y = 35 \Rightarrow y = 7$. Point: $(0, 7)$.
     • Set $y = 0$: $7x = 35 \Rightarrow x = 5$. Point: $(5, 0)$.

   • Check the origin (0,0) in both inequalities:

     • For $x + y \leq 3$, we get $0 + 0 = 0 \leq 3$, which is true.
     • For $7x + 5y \leq 35$, we get $0 + 0 = 0 \leq 35$, which is also true.

   The feasible region is bounded by the points $(0, 3)$, $(3, 0)$, $(5, 0)$, and $(0, 7)$.

2. Graph of the constraints:

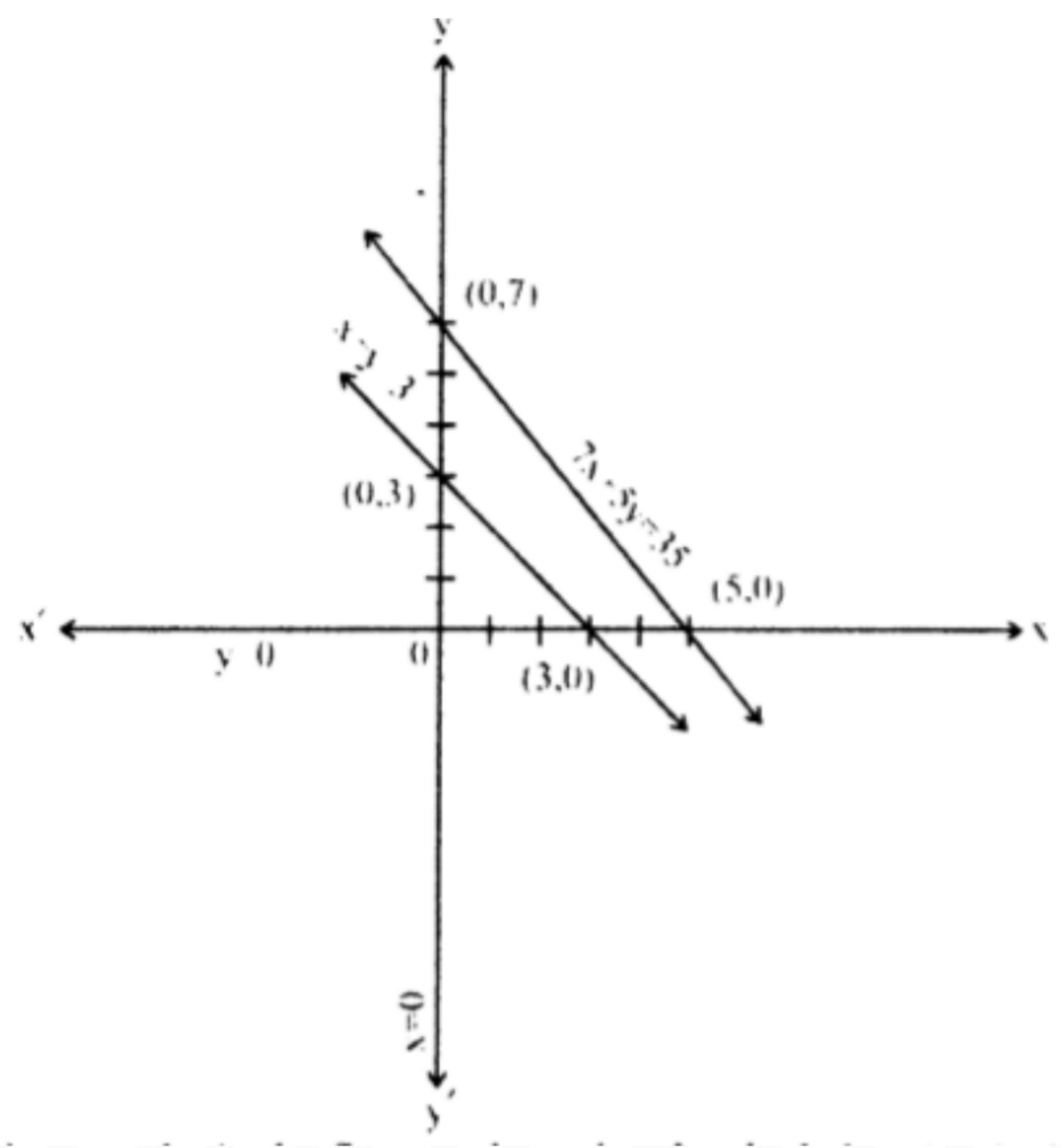
3. Corner Points: The corner points are the vertices of the feasible region:
   $(3, 0)$, $(5, 0)$, $(0, 7)$, and $(0, 3)$.

4. Evaluate the objective function at each corner point:

   • At $(3, 0)$:
     $z = 2(3) + 0 = 6$

   • At $(5, 0)$:
     $z = 2(5) + 0 = 10$

   • At $(0, 7)$:
     $z = 2(0) + 7 = 7$

   • At $(0, 3)$:
     $z = 2(0) + 3 = 3$

5. Conclusion: The maximum value of $z$ is 10, which occurs at the point $(5, 0)$.

---

Key Formulas or Methods Used

• Linear Programming: Maximize or minimize a linear objective function subject to linear constraints.
• Feasible Region: The region of the graph where all constraints are satisfied.
• Corner Point Theorem: The optimal value of a linear programming problem occurs at one of the corner points of the feasible region.

---

Summary of Steps

1. Rewrite the constraints as equalities.
2. Solve for the intersection points of the constraints.
3. Plot the feasible region on the graph.
4. Identify the corner points of the feasible region.
5. Evaluate the objective function at each corner point.
6. Determine the maximum or minimum value of the objective function.

---