6.3 Q-2

Question Statement

Prove that the straight line drawn from the center of a circle, perpendicular to a tangent, passes through the point of tangency.

---

Background and Explanation

To solve this problem, we need to understand the basic concepts of tangent lines and perpendicular lines in the context of circles. A tangent is a line that touches the circle at exactly one point, and it is always perpendicular to the radius at that point. The goal is to show that if a line is drawn from the center of the circle and is perpendicular to the tangent, it must pass through the point where the tangent touches the circle.

The general equation of a circle centered at the origin is:

$$x^2 + y^2 = r^2$$

where $r$ is the radius of the circle.

---

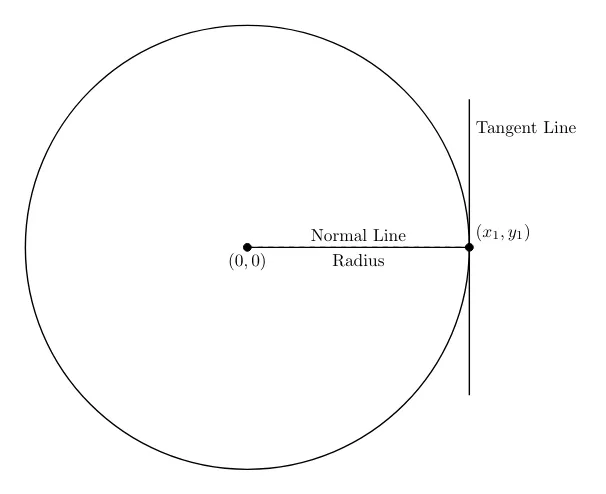
Solution

We are given the equation of a circle $x^2 + y^2 = r^2$ and a tangent to the circle at the point $(x_1, y_1)$, where the equation of the tangent is:

$$x x_1 + y y_1 = r^2$$

We need to prove that the line drawn from the center of the circle, perpendicular to this tangent, passes through the point of tangency $(x_1, y_1)$.

Step 1: Equation of the Circle and Tangent

The equation of the circle is:

$$x^2 + y^2 = r^2$$

And the equation of the tangent at the point $(x_1, y_1)$ is:

$$x x_1 + y y_1 = r^2$$

Step 2: Slope of the Perpendicular Line

The line drawn from the center of the circle is perpendicular to the tangent. The slope of the tangent at the point $(x_1, y_1)$ can be found using the equation of the tangent. The slope of the perpendicular line is the negative reciprocal of the slope of the tangent, which is:

$$\text{Slope of perpendicular line} = \frac{y_1}{x_1}$$

Step 3: Equation of the Perpendicular Line

Now, we write the equation of the line passing through the center of the circle $(0, 0)$ and having a slope of $\frac{y_1}{x_1}$. Using the point-slope form of the line equation, we get:

$$y - 0 = \frac{y_1}{x_1} (x - 0)$$

Simplifying:

$$y x_1 = y_1 x$$

Step 4: Show that the Perpendicular Line Passes Through the Point of Tangency

Now, let’s check if the perpendicular line passes through the point of tangency $(x_1, y_1)$. Substitute $x = x_1$ and $y = y_1$ into the equation $y x_1 = y_1 x$:

$$y_1 x_1 = y_1 x_1$$

This equation is true, meaning the line passes through the point $(x_1, y_1)$.

Conclusion:

Since the perpendicular line passes through the point of tangency, we have proven that the straight line drawn from the center of the circle, perpendicular to the tangent, passes through the point of tangency.

---

Key Formulas or Methods Used

1. Equation of the Circle:

$$x^2 + y^2 = r^2$$

2. Equation of the Tangent Line:

$$x x_1 + y y_1 = r^2$$

3. Slope of the Perpendicular Line:

$$\text{Slope of perpendicular} = \frac{y_1}{x_1}$$

4. Equation of the Perpendicular Line:

$$y x_1 = y_1 x$$

---

Summary of Steps

1. Write the equation of the circle and the tangent line at the point of tangency.
2. Find the slope of the line perpendicular to the tangent.
3. Use the point-slope form to write the equation of the perpendicular line passing through the center of the circle.
4. Verify that the perpendicular line passes through the point of tangency by substituting the coordinates of the point into the equation.
5. Conclude that the perpendicular line passes through the point of tangency.