6.3 Q-3

Question Statement

Prove that the midpoint of the hypotenuse of a right-angled triangle is the circumcenter of the triangle.

---

Background and Explanation

In this problem, we need to prove that the midpoint of the hypotenuse in a right-angled triangle is the circumcenter of the triangle.

To understand this, recall that the circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect. For a right-angled triangle, the circumcenter lies at the midpoint of the hypotenuse, as the hypotenuse is the longest side and the perpendicular bisectors from the other two sides meet at this point.

We will use the concept of the equation of a circle, slopes of lines, and properties of right-angled triangles to prove this.

---

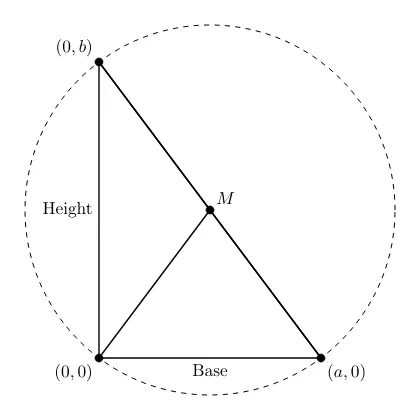
Solution

We are tasked with proving that the midpoint of the hypotenuse in a right-angled triangle is the circumcenter. Let’s proceed step-by-step.

Step 1: Equation of the Circle

Consider a right-angled triangle $ABC$ with the right angle at $C$. The equation of the circle that circumscribes this triangle is:

$$x^2 + y^2 = a^2 \tag{1}$$

where $a$ is the radius of the circle, and the center is at the origin $(0,0)$.

Step 2: Slopes of Lines $A P$ and $B P$

Let $P$ be the midpoint of the hypotenuse $AB$. The coordinates of $P$ are the average of the coordinates of points $A$ and $B$, and $P$ lies on the circle. We now calculate the slopes of the lines $AP$ and $BP$.

The slope of line $AP$ is:

$$m_1 = \frac{y - 0}{x - a} = \frac{y}{x - a}$$

Similarly, the slope of line $BP$ is:

$$m_2 = \frac{y - 0}{x + a} = \frac{y}{x + a}$$

Step 3: Perpendicularity of $AP$ and $BP$

We know that the lines $AP$ and $BP$ are perpendicular to each other, so their slopes should multiply to $-1$. Let’s check this condition:

$$m_1 \cdot m_2 = \left(\frac{y}{x - a}\right) \left(\frac{y}{x + a}\right) = -1$$

Simplifying:

$$\frac{y^2}{x^2 - a^2} = -1 \Rightarrow y^2 = -x^2 + a^2 \Rightarrow x^2 + y^2 = a^2 \tag{2}$$

This confirms that the points $A$, $B$, and $P$ satisfy the condition of being on a circle, and that $P$ lies on the circumcircle.

Step 4: Proving Equal Distances

Next, we prove that the distances from the circumcenter $C$ (the origin) to $A$, $B$, and $P$ are all equal.

1. The distance from $C$ to $A$ is:

$$|CA| = \sqrt{(x - 0)^2 + (y - 0)^2} = \sqrt{x^2 + y^2} = a$$

2. Similarly, the distance from $C$ to $B$ is:

$$|CB| = \sqrt{(x - 0)^2 + (y - 0)^2} = \sqrt{x^2 + y^2} = a$$

3. The distance from $C$ to $P$ is:

$$|CP| = \sqrt{(x - 0)^2 + (y - 0)^2} = \sqrt{x^2 + y^2} = a$$

Thus, we have shown that:

$$|CA| = |CB| = |CP| = a$$

Conclusion:

Since the distances from the center $C$ to points $A$, $B$, and $P$ are equal, we can conclude that $P$ is the circumcenter of the triangle $ABC$, and that it is the midpoint of the hypotenuse.

---

Key Formulas or Methods Used

1. Equation of the Circle:

$$x^2 + y^2 = a^2$$

2. Slope of a Line:
   $m = \frac{y_2 - y_1}{x_2 - x_1}$

3. Condition for Perpendicularity:
   $m_1 \cdot m_2 = -1$

4. Distance Formula:
   $|PA| = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

---

Summary of Steps

1. Write the equation of the circle circumscribing the triangle.
2. Calculate the slopes of the lines $AP$ and $BP$.
3. Verify that $AP$ and $BP$ are perpendicular using the condition $m_1 \cdot m_2 = -1$.
4. Prove that the distances from the center $C$ to $A$, $B$, and $P$ are all equal.
5. Conclude that $P$, the midpoint of the hypotenuse, is the circumcenter of the triangle.