6.3 Q-4

Question Statement

Prove that the perpendicular dropped from a point on a circle to a diameter is a mean proportional between the segments into which it divides the diameter.

---

Background and Explanation

In this problem, we are asked to prove a relationship involving a perpendicular dropped from a point on a circle onto the diameter. This involves the mean proportional, which is a geometric property where two segments are proportional in a specific way.

To understand this, recall that the mean proportional $G$ between two numbers $a$ and $b$ is given by:

$$G = \sqrt{ab}$$

We will use this concept to show that the perpendicular from a point on a circle divides the diameter into two segments that are in mean proportionality.

---

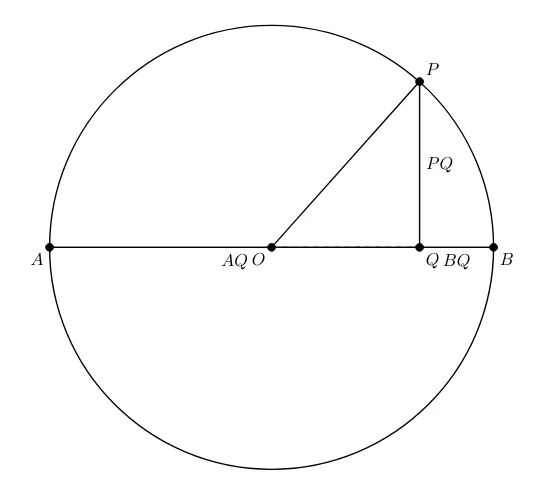
Solution

We are given a circle with the equation:

$$x^2 + y^2 = r^2$$

where $r$ is the radius of the circle. The diameter $AB$ lies along the $x$-axis, with endpoints $A(-r, 0)$ and $B(r, 0)$. A point $P(a, b)$ lies on the circle, and we drop a perpendicular from $P$ to the diameter $AB$, which intersects the diameter at point $Q$.

Step 1: Equation of the Circle and the Perpendicular Line

Since $P(a, b)$ lies on the circle, the equation of the circle gives:

$$a^2 + b^2 = r^2 \tag{1}$$

The perpendicular from $P$ to the diameter $AB$ is a vertical line, so its equation is simply:

$$x = a$$

The foot of the perpendicular, point $Q$, has coordinates $(a, 0)$, as it lies on the diameter.

Step 2: Length of the Perpendicular

The length of the perpendicular from $P$ to the diameter is the distance from $P(a, b)$ to $Q(a, 0)$. This distance is:

$$|PQ| = |b|$$

Therefore, the square of the length of the perpendicular is:

$$|PQ|^2 = b^2$$

Step 3: Using the Circle’s Equation

Since $P(a, b)$ lies on the circle, we can substitute into the equation of the circle:

$$a^2 + b^2 = r^2$$

Rearranging, we get:

$$b^2 = r^2 - a^2 \tag{2}$$

Step 4: Distances from $Q$ to $A$ and $B$

Next, we calculate the distances from point $Q$ to points $A$ and $B$ along the diameter.

1. The distance from $A(-r, 0)$ to $Q(a, 0)$ is:

$$|AQ| = |r + a|$$

2. The distance from $B(r, 0)$ to $Q(a, 0)$ is:

$$|BQ| = |r - a|$$

Step 5: Mean Proportionality

Now, we need to show that the two segments $|AQ|$ and $|BQ|$ are in mean proportionality to the length of the perpendicular $|PQ|$.

We start by finding the product of the distances $|AQ|$ and $|BQ|$:

$$|AQ| \cdot |BQ| = (r + a)(r - a) = r^2 - a^2$$

Using equation (2), we know that:

$$r^2 - a^2 = b^2$$

Thus, we can rewrite the product of the segments as:

$$|AQ| \cdot |BQ| = b^2$$

Step 6: Conclusion

Finally, recall that the mean proportional of two segments is defined as the square root of their product. Therefore, we have:

$$|PQ|^2 = |AQ| \cdot |BQ|$$

This shows that the perpendicular $PQ$ is the mean proportional between the segments $AQ$ and $BQ$, as required.

Thus, we have proven that the perpendicular dropped from a point on a circle to a diameter is a mean proportional between the segments into which it divides the diameter.

---

Key Formulas or Methods Used

1. Equation of the Circle:

$$x^2 + y^2 = r^2$$

2. Mean Proportional:

$$G = \sqrt{ab}$$

3. Distance Formula:
   $|PQ| = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

---

Summary of Steps

1. Write the equation of the circle and the perpendicular line.
2. Find the length of the perpendicular from the point to the diameter.
3. Use the circle’s equation to express $b^2$ in terms of $a^2$ and $r^2$.
4. Calculate the distances from $Q$ to $A$ and $B$.
5. Show that the product of the distances $|AQ|$ and $|BQ|$ equals $b^2$.
6. Conclude that the perpendicular is the mean proportional between the two segments.