6.4 Q-3

Question Statement

Find the equation of a parabola with its focus at the origin and its directrix parallel to:

1. The x-axis.
2. The y-axis.

---

Background and Explanation

A parabola is defined as the set of points equidistant from its focus and directrix. Depending on the orientation of the directrix, the parabola opens either vertically or horizontally. The general forms of a parabola are:

1. When the directrix is parallel to the x-axis, the parabola opens upwards or downwards, and the equation takes the form:

$$x^2 = 4ay$$

2. When the directrix is parallel to the y-axis, the parabola opens left or right, and the equation takes the form:

$$y^2 = 4ax$$

---

Solution

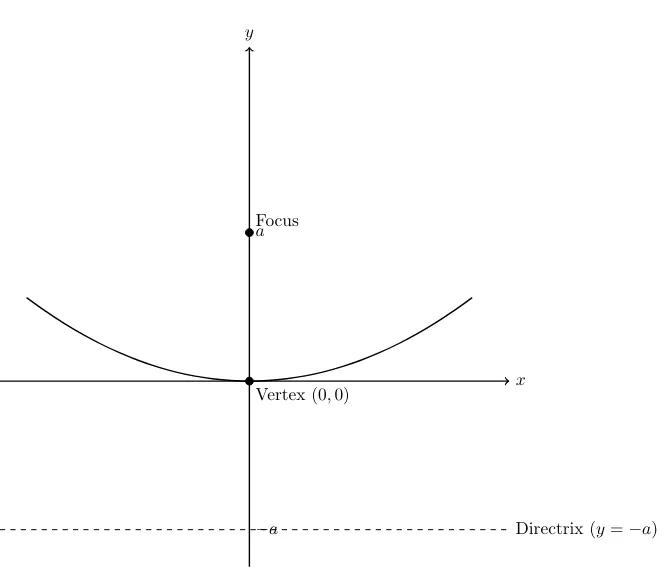
Part (i): Directrix parallel to the x-axis

1. Directrix:
   The equation of the directrix is $y = a$.

2. Focus:
   The focus is at the origin $(0, 0)$.

3. Definition:
   For any point $P(x, y)$ on the parabola, the distance to the focus is equal to the distance to the directrix:

$$|PF| = |PM|$$

4. Distance to Focus:
   The distance from $P(x, y)$ to the focus $(0, 0)$ is:

$$|PF| = \sqrt{x^2 + y^2}$$

5. Distance to Directrix:
   The perpendicular distance from $P(x, y)$ to the directrix $y = a$ is:

$$|PM| = |y - a|$$

6. Equating Distances:

$$\sqrt{x^2 + y^2} = |y - a|$$

7. Squaring Both Sides:

$$x^2 + y^2 = (y - a)^2$$

8. Simplify:

$$x^2 + y^2 = y^2 - 2ay + a^2$$ $$x^2 = -2ay + a^2$$

9. Rearrange:

$$x^2 = -2a\left(y - \frac{a}{2}\right)$$

10. Conclusion:
    The equation of the parabola is:

$$x^2 = 4ay$$

Diagram

---

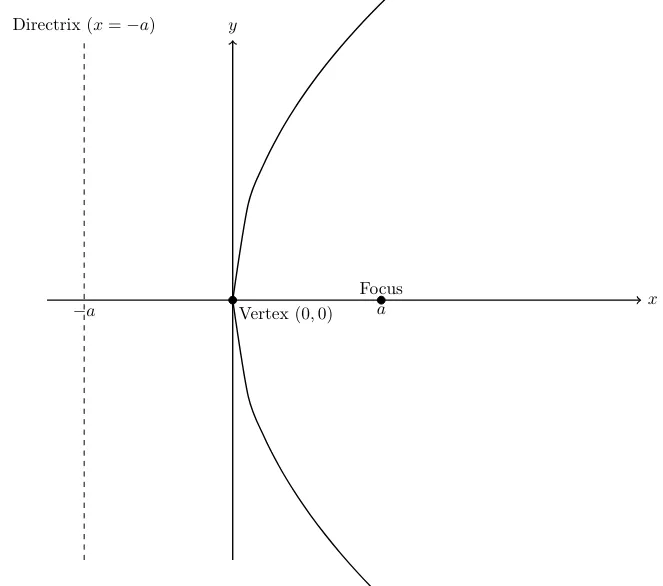
Part (ii): Directrix parallel to the y-axis

1. Directrix:
   The equation of the directrix is $x = a$.

2. Focus:
   The focus is at the origin $(0, 0)$.

3. Definition:
   For any point $P(x, y)$ on the parabola, the distance to the focus is equal to the distance to the directrix:

$$|PF| = |PM|$$

4. Distance to Focus:
   The distance from $P(x, y)$ to the focus $(0, 0)$ is:

$$|PF| = \sqrt{x^2 + y^2}$$

5. Distance to Directrix:
   The perpendicular distance from $P(x, y)$ to the directrix $x = a$ is:

$$|PM| = |x - a|$$

6. Equating Distances:

$$\sqrt{x^2 + y^2} = |x - a|$$

7. Squaring Both Sides:

$$x^2 + y^2 = (x - a)^2$$

8. Simplify:

$$x^2 + y^2 = x^2 - 2ax + a^2$$ $$y^2 = -2ax + a^2$$

9. Rearrange:

$$y^2 = -2a\left(x - \frac{a}{2}\right)$$

10. Conclusion:
    The equation of the parabola is:

$$y^2 = 4ax$$

Diagram

---

Key Formulas or Methods Used

1. Definition of a Parabola:
   For any point $P(x, y)$, the distances to the focus and directrix are equal:

$$|PF| = |PM|$$

2. Distance Formula:

$$|PF| = \sqrt{(x - h)^2 + (y - k)^2}$$

3. Perpendicular Distance to a Line:

$$|PM| = \frac{|Ax + By + C|}{\sqrt{A^2 + B^2}}$$

4. Standard Forms of Parabolas:
   • Horizontal opening: $y^2 = 4ax$
   • Vertical opening: $x^2 = 4ay$

---

Summary of Steps

1. Identify the orientation of the directrix (parallel to x-axis or y-axis).
2. Write the equation for the distances $|PF|$ and $|PM|$.
3. Equate the distances and square both sides.
4. Simplify to derive the standard equation of the parabola.
5. Identify the parameters ($a$) to determine the vertex and orientation.
6. Sketch the graph based on the equation.